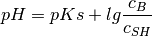Science

This program is based on the standard equations of physical chemistry, mainly taken from “the atkins” [1] .

If any deviations were made, they are explaind in this documentations and in the source code.

The detailed implementation is given in the code section.

Currently the program describes the nucleation and growth of calcium phosphate. In the long run, it is supposed to provide answers for further ions.

[1]	Peter Atkins and Julio de Paula, Physical Chemistry, 8th Edition, Oxford University Press, 2006

General procedure

1. The input are parameters are read

   • ions: charge, radius, concentration
   • solution: volume, temperature, pressure
   • special values: solubility product, ion ratios in cluster, energies
   • later: proteins and colloids as classes

2. Basic values are calculated

   • current solubility product
   • supersaturation
   • ion activity

3. As time goes by, a loop runs, calculating and logging:

   • time step (event, time step before)

   • protonation of ions in solution (pH, pKs of ions)

   • activity coefficient of ions in solution (A = 0.509, zp = 2, zn = -2, I = 1, B = 1, C = 0.01)

   • supersaturation (given pK of solid phase)

   • energy to pass critical nucleation radius (radius, factor, energy)

   • numbers of (new) germs Arrehnius equation (temp, dGn, supersat, factor)

   • call cluster function

     • add or remove ion (depending on supersat)
     • move H out of cluster (depending on age, charge, ration and size)
     • return new cluster and ion in out

   • call hyd shell function

     • add, remove H

   • calc new solution conc

   • calc new nernst layer

As result, various values over time may be collected and can be plotted in a pretty graph.

Event

An event is

1. a new cluster occurs
2. growing and shrinking cluster
3. deprotonation of phosphate in cluster

All events per loop are recorded in an list called events. At the start of each loop they will be used to estimate a reasonable time step for the next loop. during the loop, they are simply collected.

0	1	2
deprotonation	how often does	in which loop
in cluster	this occur	did it occur

Ions

A set of typical ions is included and may be extended, following the given format.

pH

Henderson Hasselbach:

(1)

Concentration

The concentration of the ions has to be given with the input files. As the concentrations change permanently, the solubility product (SP) is calculated each time it is needed:

(2)

Supersaturation

The supersaturation is calculated as follows:

(3)

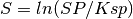
Were S is the supersaturation, SP is the solubility product and Ksp the saturation of a given salt as given in the input files.

Acitcity

The activity is described as suggested by the extended Debye-Huckel eqation:

(4)

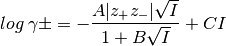
B and C are dimensionless constants, empirical parameter (values 0 ... 2..5). (Atkins 8th ed. p.165)

Nucleation

Critical energy

Following the classical nucleation theory, the enegy needed to form a mineral germ is calculated as follows [2] :

(5)

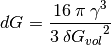
Depending on the input parameter, an alternative way to calculate dGcrit is given:

(6)

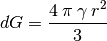
From the scientfic point of view, these are identical. gamma: surface tension, Gvol: energy per unit volume, r critical radius.

[2]	Mullin, Crystallization, 4th Edition, University of London, 2001, Butterworth-Heinemann

Nucleation rate

First, a simple homogenous nucleation is implemented.

The number of new germs is calculated, using a Arrhenius equation:

(7)

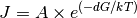
While A represents an operator, dependent on the environment. As A is only needed when calculating J, it is alway aquired directly before J. Currently A depends only the supersaturation.

Note

The more advanced heterogenous nucleation will follow.

Cluster

The culsters grow by adding ions. Before an ion is added, the following numbers are consulted:

1. supersaturation
2. hydration shell
3. desired ion ration, if given, else the charge tries to be around 0

Idea

The adsorption of ions to the wall of vessles should be respected too. In Solutions with low ion concentrations, the different materials might have a significant effect on the activity of ions.

Input of generic chemical data

Python Web Services: http://pywebsvcs.sourceforge.net/

PbubChem: http://pubchem.ncbi.nlm.nih.gov/pug_soap/examples/python_zsi/python_zsi.html

Ion

charged Particle

nucleation

assembly of ions